*Recibido: 14 Abril 2011

*Aceptado 4 JuLio 2011

Información trimestral de la biomasa del atún aleta amarilla (Thunus albacares) en el Océano Pacifico del Este es utilizada para evaluar el impacto del fenómeno de El Niño (ENSO) sobre la abundancia de esta especie. El período de 1967-1997 fue utilizado para el análisis de la dinámica de esta variable utilizando métodos gráficos (graficas de valores crudos y gráficas de espacio de fases). Los cálculos de los correspondientes eigenvalores permiten calcular la tasa intrínseca de crecimiento poblacional del atún en esta región, así como la óptima explotación de este recurso. Desde el año de 1967 es observada una tendencia a disminuir en la población alcanzando valores críticos debajo de sus valores de equilibrio o capacidad de sostén en la región. Esta tendencia se mantiene excepto por interrupciones ocasionales de mayores valores correspondientes a años de El Niño (ENSO). Desde 1982 correspondiente a la ocurrencia de un El Niño de gran magnitud el sistema parece rejuvenecer y contener una enorme cantidad de energía que le permite recuperarse por encima de su capacidad de sostén para finalmente después de 12 años regresar otra vez a su proceso de declinación. Los ángulos de intercepción de ambas líneas (línea de equilibrio y línea del espacio de fases), sugieren que el sistema presenta comportamientos predominantes que van de oscilatorios inestables a comportamientos caóticos, (table1). Los resultados nos dicen que el óptimo uso del recurso atunero en la región es favorecido en años después de un evento de ENSO y desfavorecido en años previos a un evento de ENSO. Estos resultados sugieren que una explotación racional de este recurso debería estar basada en capturas menores en un 13% de las capturas normales durante períodos del ENSO y de un 44% mayores en años después de ocurrido dicho evento.

Palabras Clave

Atún aleta amarilla, optimo uso de recursos naturales. El Niño (ENSO), Pacifico de Noreste, manejo de recursos naturales.

ABSTRACT

Three-month biomass dynamic of yellowfin tuna fish (Thunus albacares) in Eastern Pacific Ocean was used in order to evaluate the impact of Enso phenomenon on this species. The period 1967-1997 was selected for the analysis of the dynamics of this variable using graphic methods (graphs of crude data and space phase graphs).
Calculation of the correponding eigenvalues allowed estimation of the derived intrinsic population growth rate of tuna fish in this region as well as the optimun exploitation of this resource. From years 1967 on a decreasing trend in population is observed reaching critical values below equilibrium or maintaince capacity. This trend was maintained except for occassional interruptions of higher values corresponding with ENSO years. From 1982 on the systems seems to contain an enormous amount of energy allowing recuperation of the system above sustainance capacity to finally start the declining process. The angles of intersection of both lines (equilibrium line and phase space line) suggest that the system displays a predominant behavior going from unstable oscilation to chaotic mode, (table 1).
Results show that optimum use of tuna fish resource in this region is favorable in years following an ENSO event and unfavourable in those years previous to ENSO. These results suggest that a rational explotation of this resouce should be based on lower captures (13 % values) of the average normal captures biomass during ENSO periods and more than 44 % in years following the occurrence of this event

Keywords

Yyellowfin tuna, optimum use of resource, ENSO, North east Pacific, natural resouces management.

1. INTRODUCTION

ENSO or El Niño Southern Oscillation is a well known phenomenon characterized by interannual warming of Pacific ecuatorial waters (Timmerman, 2003). Seventy percent of the world tuna catch take place in this region and yellow fin tuna being the pedominant species of this catch (Diaz, 1992; Ortega 1998). Recent studies have found that tuna population dynamics is influenced by ENSO phenomenon.

Estimates of use ratio of this resource might contribute with required information to propose sustainable management strategies for this species in the Eastern Pacific Ocean.

While fishing has been practiced since the beginnig of civilization its scientific management dates from recent times. Pioneering work on fisheries management are the proposals by (Verhuls T 1838 and Schaefer 1954) the first one based on the logistic equation and the second on production. Variations of these two models have been proposed by (Fox 1975 and Pella and Tomlinson 1969, Walter 1973 and Schnute, 1977, 1985) based on Shaefer’s production model.

Studies of fisheries were first centered on estimation of areas of abundance such as the technique of tagging and recapture (Sparre and Venema, 1998) catch by unit effort (De Lury, 1947), mortality diferential and virtual population (Fry, 1949). Later, these studies were centered on population dynamics.

Models for the analysis of fish population dynamics may be classified in four large groups: the first group is represented by the surplus production model (Schaefer, 1954) using production as sole variable: the second group is represented by the analytical model (Ricker, 1958) which considers population as the sum of characteristics implicit in its individuals; the third group is constituted by time series models (Bazigos, 1983; González, 1986 and Sun and Yeh, 1998) using statistical methods in order to analyze historical population magnitudes; the fourth group is formed by models relating the resource with the environment (Ritter and Guzman, 1979, 1982, 1984; Ritter et al 1979; 1982, 1985; Diaz 1992 and Ortega 1998).

2. METHOD

Yellow fin tuna biomass (for a three month period) was calculated for period 1967 – 1997 and for the Eastern Pacific Ocean using information on the tuna numbers and for each group and applying the table weight/age published by the (Inter American Commission on Tropical Tuna 1998).

The Pacific Ocean is defined as the zone limited by the coast line of the Americas between 40ON and 40OS and the 150O W meridian (Fig. 1).

Raw data graphs and yellow fin tuna of space phase biomass were produced in order to identify their behavior. Stability of the system was analyzed by means of population eigenvectors and balance by (Vandermeer 1972 and Ritter et al 2004) graphic method. Finally these results were used to estimate optimum ratios of the fisheries resource.

Graphic analysis of the dynamic behavior of the system
Once a stable age distribution of the population is reached the proportional representation of each group (x) remains constant and the numbers or total biomass of the population may remain constant or either grow or decrease. Thus

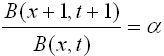Ec. 1

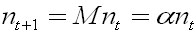Ec. 2

Where M is the community matrix,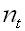 is the biomass column vector of the age groups and 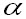is the finite rate of increment. Once the age stable distributions has been reached, 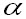transforms into the projection matrix.

Any population that has reached a stable age distribution having a communitary projection matrix with constant elements shall behave in a exponential manner.

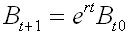Ec. 3

A repeated application of MQ-1 (where Q-1 is the inverse diagonal survival matrix ) to vector 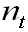shall eventually reach a point where relative proportion of elements in vector 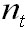will remain constant as well as constant age distribution.

However, addition of Q-1 means that the populations will reach a constant density K as stated in the logistic equation. At this point stable age distribution will reach a stationary age distribution.

Eigenvalues of matrix M are equal to antilogarithm of intrinsic rate of natural increment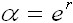
. When MQ-1n = 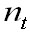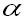is equal to one since population is in a stationary state and thus population as a whole will grow according to the logistic equation. Therefore, the populations will reach a stable age distribution when all elements of Q are equal to the dominant eigenvector of matrix M.

For small population fluctuations (measured by its communitary matrix and where time to return to balance values is measured by the real part of maximum negative eigenvector real () (max), biological stability is given by .

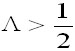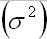
However, 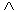ifis less than , 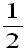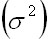one half the environmental variance, the population will suffer large fluctuations with an extintion trend. For this reason the ecosystem stability will be given by the balance of biological stability within the ecosystem and also by the magnitude of the variance of the environmental fluctuation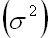 (May, 1973).

One way to analyze this dynamic behavior is to graph the population biomass in time t versus t+1 and then analyze the intersection points to a 450 straight line representing the equilibrium levels or local points of maximum carrying capacity. The slope at this point of intersection will give the eigenvalue (). When this eingenvalue is shown to be less than –1 the system is oscillatory but stable: if the eigenvalue is between 0 and +1 the system is asymptotically stable and finally if the eigenvalue is greater than +1the system is asymptotically unstable. The eigenvalues and the intrinsic rate of growth () are related according to the following expression: 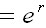in which the eigenvalue of the communitary matrix is equal to antilogarithm of intrinsic rate of natural increment ( r) (Vandermeer, 1981, Ritter et al 2004)

Determination of optimum rate of use of the fisheries resource
Let us consider the generalized logistic model given by
(Pella and Tomlinson 1969) as:

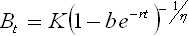Ec. 4

where 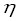is the degree of asymmetry of the production curve and the Leslie’s biomass matrix model given by

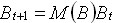Ec. 5

If B maintains the same form as the associated eigenvalues keep with the dominant eigenvalue M (B) for a specific value B, then

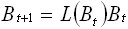Ec. 6
where L (B) is the dominant eigenvalue of M (B). It may be seen that when L (B) = 1 the population will be in equilibrium.

For the generalized logistic model Bt is discrete in our initial equation and

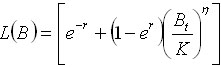Ec. 7

This form provides a connection between the generalized logistic model and Leslie’s matrix model. Thus L(B) will describe the manner in which the size of the population changes in case it would be released of being artificially maintained to a determined size.

Function L(B) is useful when evaluating the population response to different rates of explotation (H) and

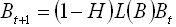Ec. 8

will be the required population in order to obtain the equilibrium size under exploitation considerations and when (1-H)L(B) = 1, with (H) having a value such that the rate of change in the size of the population reaches a maximum value and will be given by

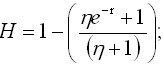Ec. 9

3. RESULTS

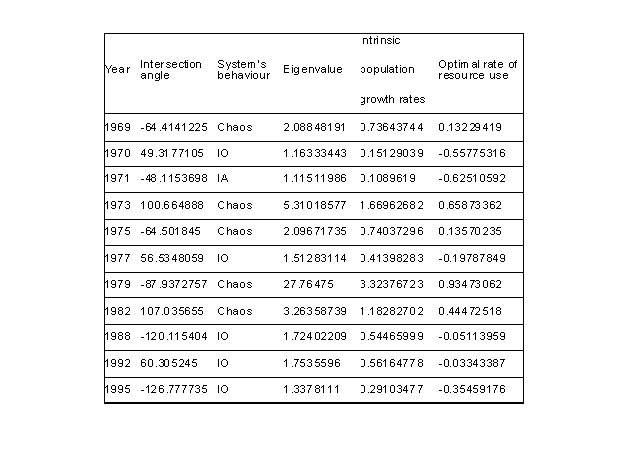
Graphic analysis of t versus t+1 of yellow fin tuna biomass showed in a period of 31 years (1967-1997) 11 intersections with the equilibrium straight line at 45o (figure 3). The slopes of these intersection lines suggest that the system has a dominant behaviour varying from unstable to chaotic (table 1) with exception of year 1971 when behaviour of the system showed an asymptotic unstable manner.
Intersections with 45o line are present in years when tuna biomass shows points of inflexion (figure 2) whereas inflexion point at minimum level are determined by a population decrement at the time of oceanic warming. Inflexion points of the valley type are determined by the increment shown by the population right after oceanic warming. Intersections with the 45o line appear before and after the ENSO events.

On yellow fin tuna biomass space phase graph are shown the various ways mentioned above in which from 1967 a decreasing trend is evident. Lowest equilibrium values (or sustainable capacity) are then displayed maintaining its tendency toward minimum values only occasionally interrupted by curls indicating the presence of an El Niño phenomenon. From 1982 the system seem to possess large energy exccedances allowing the system to recover above sustainable capacity until it reaches a natural attractor in which populations are at a maximum initiating then a process of decadence (Figure 3, table 1).

For optimum rates of the yellow fin tuna resource calculated with the table it was observed that in years before the ENSO event negative rates were present, indicating that in these years the resource should not be extracted at high rates. However, the use of the resource are positive and considerable high (from 0.13 to 0.93) allowing a greater use of the resource. It should be noted that in years when behaviour was chaotic they present also high positive rates of use and are proportional and near 90ª interseccion value.

On graph of bidimensional space phase of yellow fin tuna biomass (fig 2) a close figure behaviour was observed showing variable periodicities rotating in a counter it is clockwise direction whereas on the tridimensional space phase graph rotation on the third axis was observed in the same sense. These behaviours describe an attractor in the dynamics of this variable.

4. CONCLUSIONS

ENSO phenomenon has an impact on the yellow fin tune biomass in the Eastern Pacific Ocean. In its cool phase it may decrease population size up to 65% while in its warm phase it may be linked to a 93% increase.

Surface ocean temperature and food availability are the main factors modified by ENSO impacting on yellow fin tuna population dynamic.
Yellow fin tuna population dynamic shows a behaviour going from unstable oscillating to chaotic. It is suggested that the resource be managed with ratios from less than 13% in ENSO warm phase to ratios of up to 44% in cool phase ENSO conditions. It is hoped that results from this work will permit that the management of this resource be based on maximum sustainable yield of tuna fishenes, saving millions of dollars while preserving the resource.
The proposed methodology combines advanced simulation and optimization techniques within the fields of quantitative ecology, climate, simulation, climate change and ocean-atmosphere interactions.

While some authors have reported the influence of ENSO on the dynamics of certain fisheries like that of yellow fin tuna this relationship has not been quantified and therefore this variable had not been incorporated in models of management of this resource
Results obtained will make possible the long-term planning of the sustainable management of a relevant resource such as the yellow fin tuna.
Optimization of efforts of the fisheries fleet as well as the annual size catch will result in sustantial profits in millions of dollars for the Eastern Pacific tuna fleets, (including the Mexican) with the added benefit that the management of the resource will be based on its preservation.
ENSO is an ocean-atmosphere phenomenon affecting many natural resources; knowledge of its impact on them will allow a more rational use of these resources. Methodologies proposed in this work may be of use for the above mentioned goals.

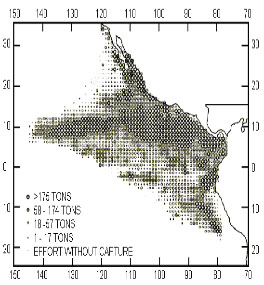
Figure 1. The Eastern Pacific Ocean and the mean captures during 1979-1993 (taken from IATTC, 1994)

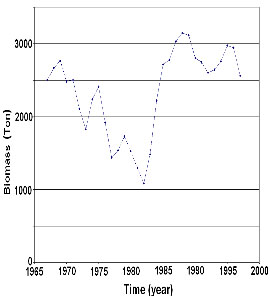
Figure 2. Yellow fin tuna fish biomass in the East Pacific Ocean, period 1967-1997.

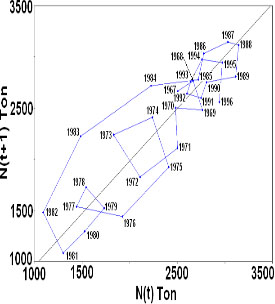
Figure 3. Biomass Nt versus N(t+1) of yellow fin tuna fish in the Easthern Pacific Ocean. Period 1967-1997.

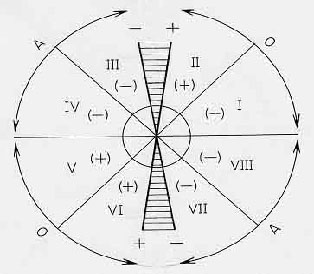
F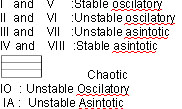

figure 4 graphic method modifyed by (Ritter et al 2004) in order to calculate phase space eigenvalues as well as the system’s behavioural patterns divided in a: oscillatory, asymptotic, stable or unstable and chaotic area.

Table 1. Estimates by graphic analysis (Vandermeer 1972 and Ritter et al (2004)) of the intersection angle, system’s behaviour, eigenvalue, intrinsic population growth and ratio of optimum use of the resource calculated by the tuna biomass dynamics for period 1967-1997 in the Eastern Pacific Ocean

5. ACKNOWLEDGEMENTS

I would like to tank Sabina Garfias Mijangos, Alfonso Salas and Alfonso Estrada for their interest and helpful encouragements.

6. REFERENCES BIBLIOGRAPHIC

Bazigos, G. P. (1983). Analysis of univariate fisheries, statistical time series. Fisheries information, data and statistical service fisheries department. Nicaragua.
Comisión Interamericana Del Atún Tropica. (1998). Informe anual. California U.S.A.-
De -Lury, DB. (1947). On the estimation of biological population. Biometrics.Vol. 3.
Diaz, P. J. (1992). Modelado de las pesquerías de túnidos en el Pacífico mexicano atún aleta amarilla). Tesis Maestría en Ciencias (Oceanografía biológica y pesquera). UNAM. 72 pp.
Fox, W.W. (1975). Fitting the generalized stock-production model by least squares and equilibrium approximation. Fish. Bull. 73: 23-37.
Fry, F. E. J. (1949) Statistics of a lake trout fishery. Biometrics, 5: 27-67.
Gonzalez, C. J. (1986). Variabilidad y predictibilidad de las capacidades de sostén y su influencia en las abundancias poblacionales del atún aleta amarilla (Thunnus albacares) de las zonas históricas de producción pesquera del océano pacífico oriental, a través del análisis de series de tiempo. Tesis. Maestría en Ciencias (Biología). UNAM. México. 90 pp.
May R. (1973). Stability in randomly fluctuating versus environments. The American Naturalist. 107(975):619-650.
Ortega, G. S. (1998). Análisis de las fluctuaciones espacio temporal en la abundancia de atún en el Océano Pacífico Oriental. Tesis Doctorado (Biología). Fac. de Ciencias. UNAM. 186 pp.
Pella, J. J. y Tomlinson, P. K. (1969). A generalized stock production model. . Inter—Americana Trop. Tuna Comm. Bull. 13(3):421-496.
Ritter, W. E. (1958). Handbook of computation for biological statistics of fish population. Bull. Fish. Res. Board Can., 199, 300 pp.
Ritter, O. W.; R. S. Guzman; C. E. Buendía Y A. T. Morales. (1979). Sobre la evaluación de los recursos naturales (aspectos ambientales en la productividad oceánica), Parte II. Anales del Instituto de geofísica. 25:135-152.
Ritter, O. W.; R. S. Guzman. (1982). Efectos meteorológicos y oceanográficos en la productividad del Océano Pacífico del Este. Geofísica. 17:23-39.
Ritter, O. W.; G. R. Klimek y R. S. Guzmán. (1982). Sobre la abundancia, distribución y comportamiento del atún aleta amarilla en el Océano Pacífico del Este y su correlación a condiciones físico-ambientales. Geofísica. 17:6-22.
Ritter. w. y r. s. Guzmán, R.S. (1984). Modelo generalizado de producción pesquera con dependencia ambiental, una aplicación en el Golfo de Tehuantepec. Geofisica. 20:21-29.
Ritter, O. W.; Jauregui, O. E.; Guzman, R.S.; Estrada, B, A.; Muñoz, N., H.;Suarez S. J. y Ma. Del Carmen corona (2004). Ecological and agricultural productivity indices and their dynamics in a sub-humid/semi-arid region from Central Mexico. Journal of Arid Environments 59, 753-769.
Schaefer, M. B. (1954). Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-Amer. Trop. Tuna Comm. Bull. 1(2):25-56.
Schnute, J. (1977). Improved estimates from the Schaefer production model: theoretical consideratons. J. Fish. Res. Bd. Canada 34: 583-603.
Schnute, J. (1985). A general theory for analysis of catch and effort data. Can. J. Fish. Aquat. Sci. 42: 414-429.
Sparre, P. y Venema, S. C. (1998). Introduction to Tropical Fish Stock Assesment. Part 1: Manual FAO, Roma.
Sun, C. L. y Yeh, S. Z. (1998). Arima modeling and forecasting the albacore catch and CPU of the Taiwanese tuna logline fishery in the South Atlantic Ocean. Acta Oceanographica, Vol. 36, NO2, 125-137.
Timmermann, A. (2003). Decadal ENSO amplitude modulations: a nonlinear paradigm. Global and Planetary change. 37:135-156.
Vandermeer, J. H. (1972). Elementary mathematical ecology. John Wiley. New York.
Verhulst, P. F. (1838). Notice sur la loi que la population pursuit dans son accroissement. Corresp. Math. Phys. 10:113-121.
Walter, E. (1973). Delay-differential equation models for fisheries. J. Fish. Res. Board Can. 30:939-945.